|
|
|
|
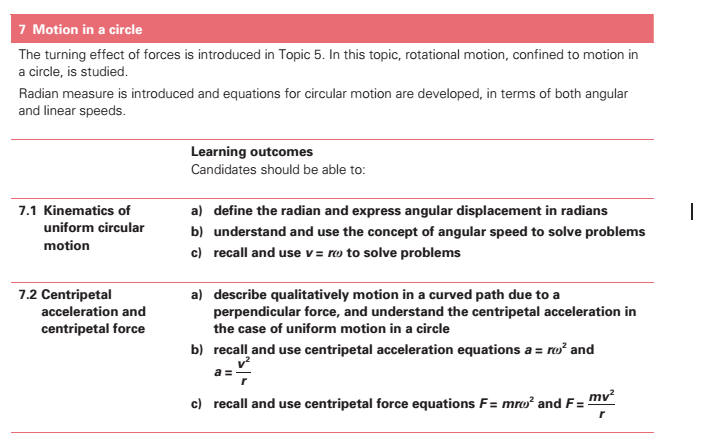
(a) express angular displacement[] in radians. (b) understand and use the concept of angular velocity to solve problems. (c) recall and use ν
= rω to solve problems. * (d) describe qualitatively motion in a curved path due to a
perpendicular force, and understand the centripetal acceleration[] in the
case of uniform motion in a circle. (e) recall and use centripetal acceleration[] a = rω2 , a = v 2 /r. (f) recall and use centripetal force[] F = m rω2 , F = mv2 /r. |
|
|
|
|
|
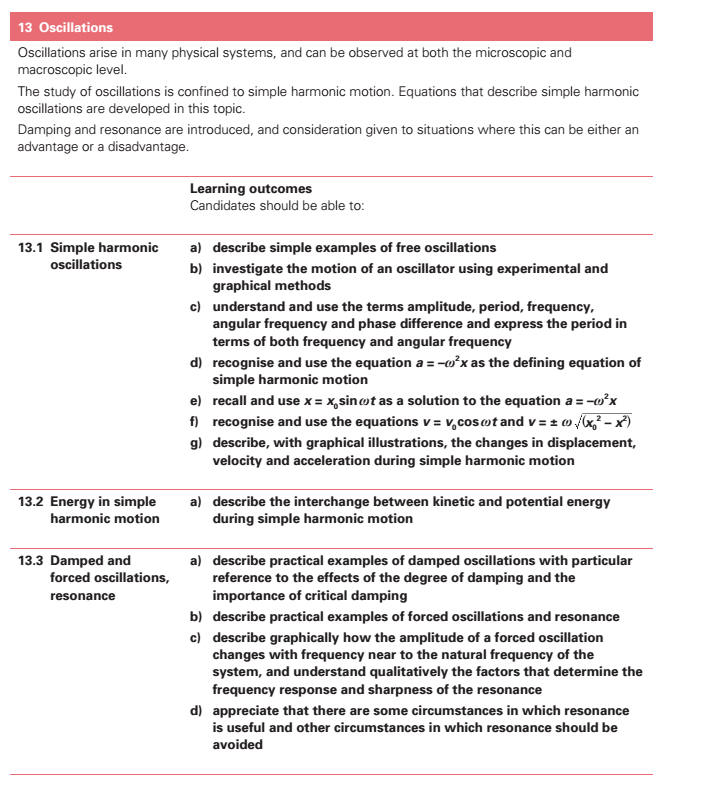
(a) describe simple examples of free oscillations. * (b) investigate the motion of an oscillator using
experimental and graphical methods. (c) understand and use the terms amplitude, period, frequency, angular
frequency and phase difference[] and express the period[][] in
terms of both frequency and angular frequency. (d) recognise and use the equation a = -ω2x as the defining equation
of simple harmonic motion - SHM[]. (e) recall and use x =
xosinωt as a solution to the equation a = -ω2x. (f) recognise and use * (g) describe with graphical illustrations, the changes in
displacement, velocity and acceleration[] during simple harmonic motion,
shm. (h) describe the interchange between kinetic and potential energy during
simple harmonic motion. * (i) describe practical examples of damped oscillations with
particular reference to the effects of the degree of damping and the
importance of critical damping in cases such as a car suspension system. (j) describe practical examples of forced oscillations and resonance. * (k) describe graphically how the amplitude of a forced
oscillation changes with frequency near to the natural frequency of
the system, and understand qualitatively the factors which determine the
frequency response and sharpness of the resonance. (l) show an appreciation that there are some circumstances in which resonance
is useful and other circumstances in which
resonance[] should be avoided. |
|
|
(a) show an understanding of the concept of a gravitational field as an example of field of force and define gravitational field strength as force per unit mass.* (b) recall and use Newtons law of gravitation in the form F = G(m1m2)/r2.(c) derive, from Newtons law of gravitation and the definition of gravitational field strength, the equationg = GM/ r2 g = for the gravitational field strength of a point mass.* (d) recall and solve problems using the equation(e) show an appreciation that on the surface of the Earth g is approximately constant and is called the acceleration[] of free fall.(f) define potential at a point as the work done[] in bringing unit mass from infinity to the point.* (g) solve problems using the equation φ = − GM/ r for the potential in the field of a point mass.(h) recognise the analogy between certain qualitative and quantitative aspects of gravitational field and electric field.* (i) analyse circular orbits in inverse square law[] fields by relating the gravitational force to the centripetal acceleration[] it causes.(j) show an understanding of geostationary orbits and their application. |
|
|
|
|
|
* (f) recall and use Coulombs law in the form F = Q1Q2/4πεor 2 for the force between two point charges in free space or air.* (g) recall and use E = Q/4πεor 2 for the field strength of a point charge in free space or air.(h) define potential at a point in terms of the work done[] in bringing unit positive charge from infinity to the point.(i) state that the field strength of the field at a point is numerically equal to the potential gradient at that point.* (j) use the equation V = Q/4πεor for the potential in the field of a point charge.(k) recognise the analogy between certain qualitative and quantitative aspects of electric field and gravitational fields.
|
|