|
|
|
|
(a) describe what is meant by wave motion as illustrated by vibration in
ropes, springs and ripple tanks. (b) show an understanding and use the terms displacement[], amplitude, phase
difference, period[], frequency, wavelength[] and speed. (c) deduce, from the definitions of speed, frequency and wavelength, the
equation
ν = fλ. (d) recall and use the equation ν = fλ. (e) show an understanding that energy is transferred due to a progressive
wave. (f) recall and use the relationship, intensity[] ∝ (amplitude)2. (g) compare transverse and longitudinal waves. * (h) analyse and interpret graphical representations of
transverse and longitudinal waves. (i) show an understanding that polarisation[] is a phenomenon associated with
transverse waves. * (j) determine the frequency of sound using a calibrated
c.r.o. * (k) determine the wavelength[] of sound using stationary
waves. * (l) state that all electromagnetic waves travel with the
same speed in free space and recall the orders of magnitude[] of the wavelengths of
the principal radiations from radio waves to
γ-rays. |
|
|
|
|
|
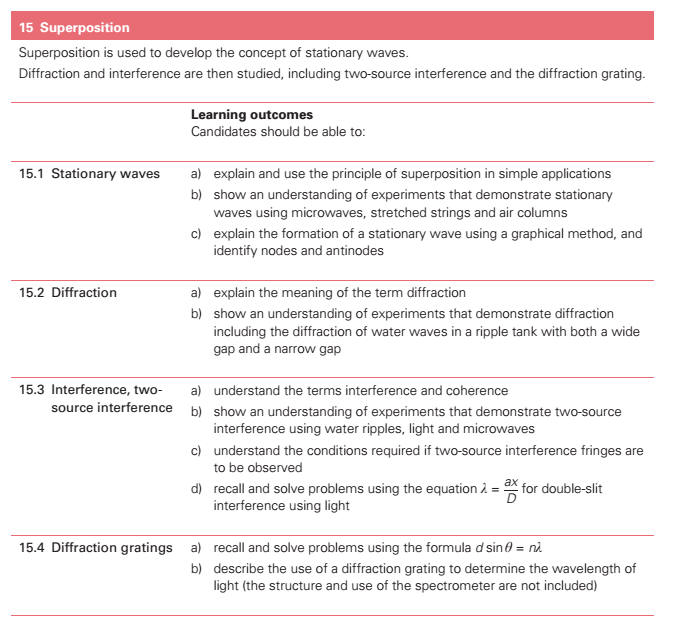
* (a) explain and use the principle of superposition in
simple applications. * (b) show an understanding of experiments which demonstrate
stationary waves[] using microwaves, stretched strings and air
columns. * (c) explain the formation of a stationary wave using a
graphical method, and identify nodes and antinodes. (d) explain the meaning of the term diffraction. (e) show an understanding of experiments which demonstrate diffraction
including the diffraction[] of water waves in a ripple tank
with both a wide gap and a narrow gap. (f) show an understanding of the terms interference and coherence. (g) show an understanding of experiments which demonstrate two-source
interference using water, light and microwaves. (h) show an understanding of the conditions required if two-source
interference fringes are to be observed. (i) recall and solve problems using the equation λ = ax
/ D for double-slit
interference using light. (j) recall and solve problems using the formula d sinθ = nλ and describe the use of a diffraction[] grating to determine the wavelength |
|