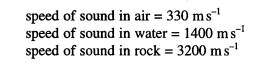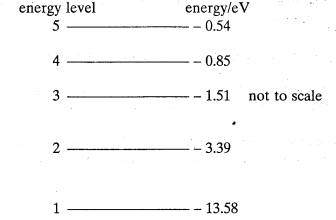PH02 Jun00 click to view mark scheme
5 Electrons
may be emitted when electromagnetic radiation is incident on a metallic
surface.
(a) The photoelectric equation is
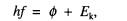
where
h is the Planck constant and f is the
frequency of the incident radiation.
Explain
the meanings of
work
function, ø …………………………………….
and
Ek ……………………………………………………….
(2)
(b) In
a typical experiment to investigate the photoelectric effect, Ek was measured
for photons of different wavelengths, l, and the values in the table were
obtained.
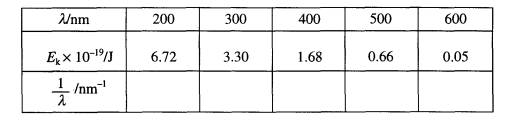
(i) By rearranging the photoelectric
equation, show that a graph of Ek (y-axis) plotted against
1/ l (x‑axis)
will give a straight line.
(ii) Use the above data to plot this graph on the grid provided and
use your graph to determine values
for ø, in eV,
and the Planck constant, h.
(c) Using
the same axes, sketch the graph which you would expect to obtain if the
experiment
were
repeated with a metal having a larger value of ø (2)
(d) In
a simple demonstration of the photoelectric effect, a metal plate is given a
negative charge and illuminated with, in turn,
(i)
red light from a laser,
(ii)
an ultraviolet lamp.
The ultraviolet lamp causes the plate to lose charge but the
laser has no effect. Explain why this is so.
(2)
=(15)
Mar 00 click
to view mark scheme
6 (a) Explain what is meant by critical angle
and total internal reflection.
(3)
(b) The
diagram shows a cylindrical optical fibre, of radius r, bent into an arc of radius R. A ray of light entering along the
axis strikes the internal surface of the fibre at an angle of incidence theta
and is internally reflected.
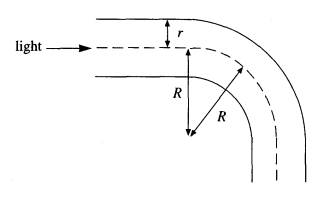
Draw
the angle theta on the diagram and hence show that
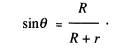
(2)
=(5)
7 (a) (i) Explain
what is meant by duality of electrons.
(ii)
Give one example of each type of behaviour
of electrons.
(3)
(b) Electrons,
of mass m and charge e, are accelerated from rest through a
potential difference, V, and acquire a kinetic energy of 1/2 mv2,
where v is the final velocity of the electrons
Show
that
l = h
Ö 2meV
where
h is the Planck constant and l
is the electron wavelength.
(3)
=(6)
Jun99 click to view mark scheme
1. In an
experiment to investigate the structure of the atom, alpha particles were aimed
at thin gold foil
in a
vacuum. A detector was used to determine the number of a. particles deflected
through
different
angles.
(a) State two observations about the alpha
particles detected coming from the foil.
(2)
(b) State two features of the structure of the
atom which can be deduced from these observations.
(2)
=(4)
2 (a) Nuclear fission can occur when a neutron
is absorbed by a nucleus of uranium‑235.
An
incomplete equation for a typical fission reaction is given below.
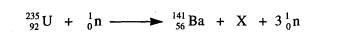
(i) State the nuclear composition of X.
proton
number
..................................................................................................................
neutron
number
................................................................................................................
(ii) Name the element of which X is an isotope.
=(3)
4 Sonar is a
method of detecting underwater objects by transmitting a pulse of ultrasound
and detecting the reflected pulse. An anchored sonar buoy is immersed in water,
as shown in the diagram, and sends out waves in all directions.
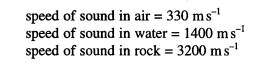
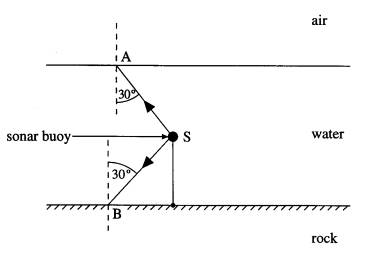
(a) Explain whether or not total internal
reflection can occur for sound waves at
(i)
the water-air interface,
(ii)
the water-rock interface.
(3)
(b) Explaining your answers, sketch on the
diagram the directions of sound waves initially
travelling in the
directions
(i) SA, after reaching the water surface,
(ii)
SB, after reaching the water-rock
interface.
(5)
=(8)
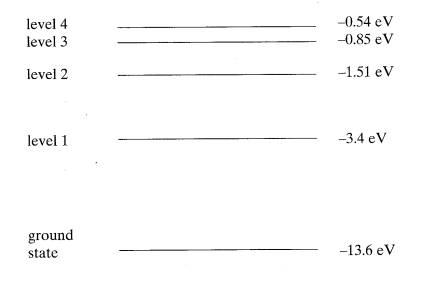
6
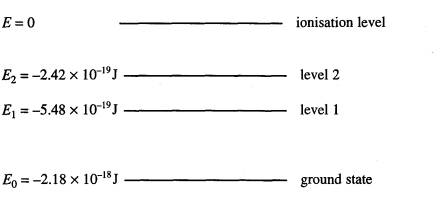
The diagram
represents some of the energy levels of an isolated atom. An electron with a kinetic energy of
2.0 x 10‑18J
makes an inelastic collision with an atom in the ground state.
(a) Calculate the speed of the electron just
before the collision.
(2)
(b) (i) Show
that the electron can excite the atom to level 2.
(ii) Calculate the wavelength of the radiation that will result when
an atom in level 2 falls to level 1 and state the region of the spectrum to
which this radiation belongs.
(6)
(c) Calculate
the minimum potential difference through which an electron must be accelerated
from rest in order to be able to ionise an atom in its ground state with the
above energy level structure.
(2)
=(10)
7 (a) Calculate
the speed of electrons which have a de Broglie wavelength of 1.5 x 10‑10m.
(2)
(b) Would
you expect the electrons in part (a) to be diffracted by crystals in which the
atom spacing is 0.10nm? Explain your answer.
(2)
=(4)
Mar99 click to view mark scheme
6 A small
intense light source is 1.5 m below the surface of the water in a large
swimming pool, as shown in the diagram.
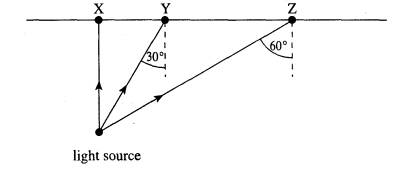
(i) Complete
the paths of rays from the light source which strike the water surface at X, Y
and Z.
(ii) Calculate
the diameter of the disc through which light emerges from the surface of the
water.
speed of
light in water = 2.25 x 108 m s-1 speed of light in air = 3.00
x 108 m s-1
=(7)
7 Use data
from the Data sheet in this question.
(a) (i) Define
the electronvolt.
(ii) Show that the speed of an electron
accelerated through a potential difference of 6.0kV is
4.6 x 1 07m
(4)
(b) State what is meant by the duality of the
nature of electrons.
(1)
(c) In
a demonstration of electron diffraction, a narrow beam of electrons is
accelerated through 6.0kV and passes normally through a thin film of graphite mounted
in a vacuum tube. Concentric rings appear on a fluorescent screen at the end of
the tube.
(i) Calculate the wavelength associated with
the electrons.
(ii) What information does your answer to part (c)(i) suggest about
the spacing of carbon atoms in graphite?
(4)
=(9)
June98 click
to view mark scheme
4 (c) The first of
the spectral lines in part (a) (435 nm) corresponds to one of the lines in the
spectrum of atomic hydrogen. The energy level diagram below represents, the
first five energy levels for this spectrum. Determine which of the energy level
transitions will give this spectral line.
(4)
5 (a) Calculate
the wavelength of a gamma‑ray photon which has an energy of 1.6 x 10‑15
J
(2)
(b) An
X‑ray photon is generated which has the same energy as the gamma‑ray
described in part (a). Compare these two photons in respect of their
(i)
speed of transmission in a vacuum,
(ii) ability to penetrate a given material.
(2)
=(4)
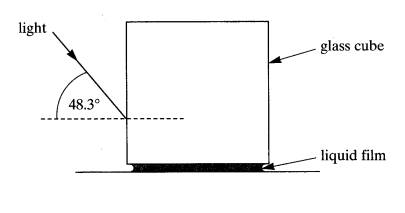
6 The Einstein photoelectric equation is
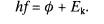
(a) State the meaning of each of the terms in the
equation.
(3)
(b) In a
laboratory demonstration of the photoelectric effect, a metal plate is given an
electric charge and light of various wavelengths is shone on to the surface of
the plate in turn. It is found that the plate loses its electric charge when
the plate is given a negative charge and when ultraviolet light is shone on to
the plate.
Explain why
the plate does not lose its charge when
(i) the plate is given a positive charge and
illuminated by ultraviolet light,
(ii) the
plate is given a negative charge and illuminated by visible light.
(4)
=(7)
Mar 98 click to view mark scheme
1 (a) Describe the principal features of the nuclear model of the atom suggested by Rutherford.
(4)
(b) When
gold foil is bombarded by alpha particles it is found that most of the
particles pass through the foil without significant change of direction or loss
of energy. A few particles are deviated from their original direction by more
than 90^o Explain, in terms of the nuclear model of the atom and by considering
the nature of the forces acting,
(i) why some alpha particles are deflected
through large angles,
(ii) why most of the alpha particles pass through the foil without any
significant change in direction or significant loss of energy.
(5)
=(9)
6 The diagram
shows a cube of glass which is placed on a horizontal surface. The lower face
of the cube is separated from the surface by a film of liquid. A ray of light
from outside the glass strikes a vertical face of the cube at an angle of
incidence of 48.3o After refraction, this ray is just totally
internally reflected at the critical angle at the glass‑liquid interface.
refractive
index of glass = 1.5
(i) On the diagram, sketch the path of the ray
through the glass cube.
(ii) Calculate the critical angle at the glass‑liquid
interface.
(iii) Calculate the refractive index of the
liquid.
(6)
=(6)
7 (a) When electrons collide with atoms, the
atoms may be excited or may be ionised.
Explain
what is meant by
(i)
excitation by collision,
(ii)
ionisation by collision.
(3)
(b) Explain, in terms of what happens to the
atom, how the lines in an atomic line spectrum are produced.
=(7)
Jun 97 click
to view mark scheme
7 The spacing of
atoms in a crystal is 1.0 x 10-10
m.
mass of the electron 9.1 x
10-31 kg
the
Planck constant 6.6
x 10-34 J S
(a) Estimate the speed of electrons which would
give detectable diffraction effects with such crystals.
(3)
(b) State
and explain how the speed of electrons would have to be different in an
experiment to observe their diffraction by atomic nuclei.
(2)
(c) Give two pieces of evidence to demonstrate
that electrons have particle properties.
(2)
=(7)
Feb 97 click to view mark scheme
2 (a) In the photoelectric effect equation
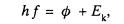
explain
what is meant by
hf
E k
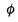
(6)
(b) Monochromatic
light of wavelength 500 nm falls on a metal cathode of area 2000 mm2 and
produces photoelectrons. The light intensity at the surface of the metal is 1.0
x 10-2 W m-2.
charge of
electron = -1.6 x 10-19 C
the Planck
constant = 6.63 X 10-14 J S
speed of
light in vacuo = 3.0 x 108 ms‑1
Calculate
(i)
the frequency of the light,.
(ii) the energy of a single photon of the
light,
(iii) the number of photons falling on one square
millimetre of the metal in one second,
(iv) the total photoelectric current, assuming
that each photon releases one photoelectron.
(9)
=(15)
6 (a) Light
travelling in a medium of refractive index n1
is incident on the boundary with a medium of refractive index n2
State the circumstances
under which total internal reflection
occurs.
(2)
(b) (i) Calculate
the critical angle for a water-air boundary if the refractive index of
water is 1.33.
(ii) A fish in a pond is swimming directly below a small boat which is
12 m from the shore. Calculate the minimum depth of the fish in the water for
it to be able to see the ankles of a fisherman standing on the edge of the
water.
(4)
=(6)
Jun 96 click
to view mark scheme
2 The diagram shows a glass pentaprism as
used in the viewfinder of some cameras. Light enters face AB and leaves face
BC. The faces AE, ED and DC are silvered and the refractive index of the glass
Is 1.52.
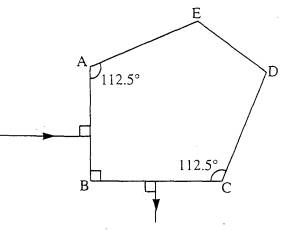
(a) On the
diagram above draw the path of the incident ray from face AB to face CD,
(b) State why
you have drawn the ray in this direction.
(c) Explain,
with the aid of a calculation, why the face CD needs to be silvered if the ray
shown is not to be refracted at face CD.
(3)
(d) On the
diagram, continue the ray until it leaves the prism.
(1)
=(6)
6 A monochromatic light source provides 5 W
of light of wavelength 4.50 x 10-7 m. This light falls on a
clean potassium surface and liberates 3.2 x 1011 photoelectrons
per second.
The photoelectrons
are collected by an electrode just above the metal surface and the
photoelectric current measured.
charge of electron = -1.60 x 10-19
C.
speed of
light in vacuo = 3.00 x 108 ms
(a) Calculate the photoelectric current given
by this arrangement.
(b) Estimate
the photoelectric current given by a similar arrangement using a source which
provides 10 W of light of wavelength 4.50 x 10 -7 m.
(2)
(c) Explain
whether or not photoelectrons would be emitted if a 20 W source operating at a
wavelength of 6.00 x 10-7 m were to be used. The threshold
frequency for potassium is 5.46 x 1014 Hz.
(3)
=(6)
7 (a) With reference to electron energy levels in
atoms, explain what is meant by
(i) excitation
(ii) ionisation
(b) The diagram below represents the energy
level diagram for atomic hydrogen.
(i)
Calculate the ionisation energy in
joule.
(ii) Calculate the wavelength emitted for the transition n=3 to n=2.
iii) Calculate the energies of the photons which could be emitted after
a hydrogen use only atom in its ground‑state gains 12.08 eV
(6)
=(9)
Feb 96 click to view mark scheme
3 (a) When
alpha particles are projected at a thin metal foil in a vacuum enclosure they
are scattered at various angles.
(i) In which direction will the maximum number of alpha particles
coming from the foil be detected?
(ii)
Describe the angular distribution of
the scattered alpha particles around the foil.
(iii)
What do the results suggest about the
structure of the metal atoms?
(5)
(b) In this arrangement explain why
(i) the foil should be thin,
(ii)
the incident beam of a particles should be parallel and narrow.
(2)
=(7)
7 (a) Explain the meaning of the term represented
by the symbol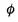 
in the photoelectric
equation.
(2)
(b) Monochromatic
light of wavelength 3.80 x 10-7 m falls with an intensity of
6.0 mW m-2 on to a
metallic surface whose work function is 3.2 x 10-19 J
Using data from the Data
Booklet calculate
(i) the energy of a single photon of light of
this wavelength,
(ii) the number of photoelectrons emitted per second from 1.0 mm2
of the surface if a photon has a 1 in 1000 chance of ejecting an electron,
(iii) the maximum kinetic energy which one of these photoelectrons
could possess.
(4)
=(6)
Jun 95 click to view mark scheme
5 In surveying
the Earth for oil, longitudinal waves are generated at the air/rock interface,
and travel into the rock where they may be refracted and reflected.
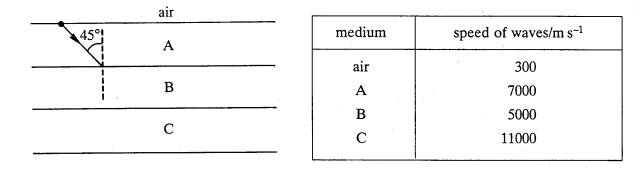
The diagram
shows a narrow beam of waves directed into three horizontal, parallel layers of
rock, A, B and C. The beam is incident on the AB boundary at 45o to
the vertical, as shown. The speed of the waves in each medium is given in the
table.
(a) Calculate
(i)
the refractive index for waves
travelling from A to B,
(ii)
the angle of incidence on the BC
boundary.
(3)
(b) (i) With
the help of a calculation, show that total internal reflection will occur at
the BC boundary.
(ii) Redraw the diagram, showing the complete path of the beam in the
rock, and the magnitude of the angles.
State, with a reason,
whether the waves will emerge into the air.
(4)
=(7)
6 Use data
from the data booklet in this question.
The diagram
represents the lowest energy levels of the electron in the hydrogen atom on a
scale in which the energy of an electron completely free of the atom is zero.
Level 1 is the ground state.
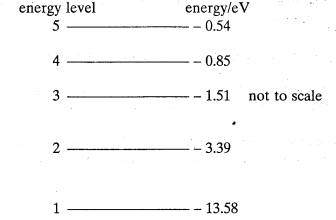
(a) Calculate the ionisation energy, in J of
the hydrogen atom.
(b) Excitation
of the hydrogen atom may be produced if an electron of energy 11.50 eV collides
with the atom.
(i)
Explain what is meant by excitation
in this context,
(ii) Calculate the maximum energy of the electron in eV after a
collision producing excitation.
(3)
(c) Calculate
the wavelength of the radiation associated with the transition from level 3 to
level 1. In. which region of the electromagnetic spectrum does this line lie?
(The
approximate wavelength range of the visible spectrum is from 400 nm to 700 nm.)
(3)
=(7)
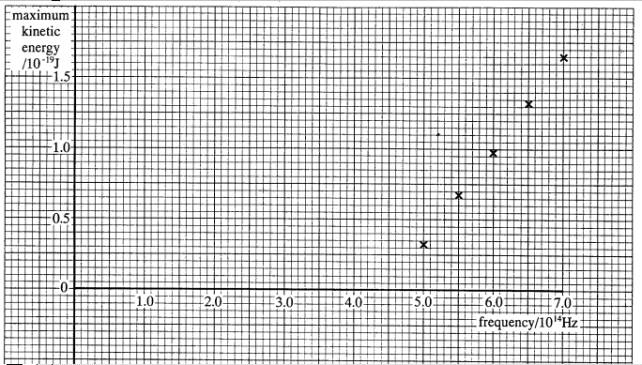
7 The points
plotted on the graph opposite show the results of an experiment in which the
frequency of the radiation falling on a metal surface was varied, and the
maximum energy of the photoelectrons emitted was measured.
(a) Explain what is meant by the work function
of a metal.
(b) (i) Determine
the gradient of the best straight line through the points on the graph, and the
intercept on each axis.
(ii) State Einstein's photoelectric equation, and show that the
experimental results are consistent with it.
(iii)
Deduce the work function of the metal
used in the experiment.
(6)
(c) (i) Calculate
the maximum wavelength which would cause this metal to emit electrons.
(ii) Name one other kind of electromagnetic radiation, apart from
the visible spectrum, which would cause this metal to emit electrons. Justify
your answer in terms of the quantum theory. (3)
speed
of light, c, = 3.00 x 108 ms‑1
(4)
=(10)
March 95 click to view mark scheme
3 (a) (i) State what was observed in Rutherford's experiments
on the scattering of a particles by
thin gold foil.
(ii) Explain how these results were important in establishing the
structure of the
atom.
4
4 (a) Sketch
and explain briefly a simple experimental arrangement that may be used to demonstrate
that when visible or ultraviolet light is shone on to the clean surface of
certain metals, electrons are emitted.
3
(b) Use data from the data booklet in this
question.
When light of wavelength 4.5 x
10-7 m falls on the clean surface of sodium metal electrons
are emitted from the surface. The maximum kinetic energy these electrons can
possess is observed to be 1.9 x 10-19 J, and to be independent
of the intensity of the incident light.
(i) In terms of the quantum theory of light, explain why the
emitted electrons have a maximum value of kinetic energy.
(ii) Explain why this maximum is independent of the intensity of the
light incident on the surface.
(iii)
Calculate the energy of a photon of
light of wavelength 4.5 x 10-7 m
(iv) Hence determine the frequency of incident light below which no
electrons will be emitted from sodium.
7
=10
5 Light is
emitted when the vapour of an element is bombarded by energetic electrons. The
spectrum of
the light emitted contains lines each of a definite wavelength.
(a) Explain how energetic electrons cause the
atoms of the vapour of an element to
emit
light.
3
(b) How does the existence in the spectrum of
lines of a definite wavelength support the
view
that atoms have discrete energy levels?
2
=5
6 The diagram
below shows a horizontal rectangular tank containing water. A plane mirror is
placed at an angle to the bottom surface of the tank.
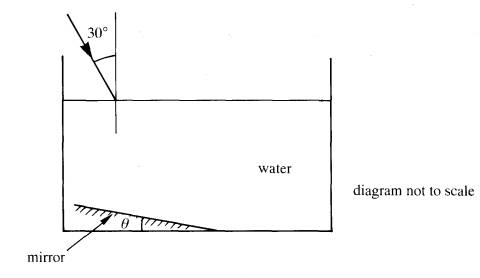
A ray of
light is incident on the surface of the water at an angle of 30o as
shown.
(a) For'
small values of the angle q the ray is reflected from the surface of the mirror
and emerges at a point on the surface of the water. Redraw the diagram in your
answer book and show the path of the ray of light through the liquid and after
it has emerged from the water surface.
3
(b) Using data from a data booklet,
calculate
(i)
the angle of refraction for the ray
as it enters the water,
(ii) the critical angle at a water air
boundary.
3
(c) For
a particular value of the angle 0, the reflected ray is incident on the water
surface at the critical angle.
Calculate
this angle 0.
2
=8
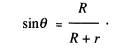